扫码添加助教

免费领取

备考资料大礼包

扫码关注公众号

SAT数学Problem Solving练习题(1)

2013-07-30 16:00:07来源：网络

【考试动态】2019年SAT考试时间报名费用报考指南成绩查询送分流程成绩要求成绩换算
【资料推荐】SAT词汇巴朗3500系列SAT阅读OG1-8经典错题解析SAT数学满分冲刺重要知识点
【备考指导】CB发布2018年SAT考试官方报告SAT北美考点汇总美国大学TOP100SAT成绩要求

　　下面新东方在线为大家整理了SAT数学Problem Solving练习题(1)，供考生们参考，以下是详细内容。

　　Question #1: If a · b = 18 and a / b = 2, a > 0, b > 0 then:

　　(a) a = 18 and b = 1

　　(b) a = 9 and b = 2

　　(d) a = 6 and b = 3

　　(e) a = 6 and b = 6

　　Answer: a / b = 2

　　a = 2·b.

　　a·b = (2· b)· b

　　a·b = 2· b 2.

　　2· b 2 = 18

　　b 2 = 9,

　　b = 3 because b > 0,

　　a = 2· b

　　a = 6.

　　Question #2: The ratio of the radii of two circles is r1/r2 = 6. What is the ratio of the perimeters P1/P2 and the ratio of the areas of the two circles A1/A2?

　　(a) perimeter ratio = 1/6, area ratio = 36

　　(b) perimeter ratio = 36, area ratio = 6

　　(d) perimeter ratio = 1/8, area ratio = 8

　　(e) perimeter ratio = 1/6, area ratio = 6

　　Answer: r1 / r2 = 6;

　　Perimeter1 / Perimeter2 = (2· ¶· r1)/(2· ¶· r2) = r1/ r2 = 6

　　Area1 / Area2 = (¶· r12)/ (¶· r22) = r12 / r22 = 36

　　Question #3: What value x satisfies both 1/x < 1/7 and x 2 > 16?

　　(a) x = 1

　　(b) x = -5

　　(d) x = 7

　　(e) x = 6

　　Answer: x 2> 16 means (x - 4)· (x + 4) > 0.

　　x can be lower than -4 or higher than 4.

　　1/x < 1/7; (7-x) / 7x < 0.

　　x can be lower than 0 or higher than 7.

　　In conclusion, x can be lower than -4 or higher than 7. The only correct answer is x = -5.

　　Question #4: A lottery sells 1000 tickets and there is only one winning number. 200 New Jersey residents buy 2 tickets each, 300 New York

　　residents buy 1 ticket each and the rest are sold in Connecticut. What is the probability that the wining ticket was bought in New Jersey?

　　(a) 3/5

　　(b) 1/2

　　(d) 1/5

　　(e) 4/5

　　Answer: There are 400 tickets sold in New Jersey out of a total of 1000, so the probability will be 400/1000 = 2/5.

　　Question #5: Celsius degrees can be transformed in Fahrenheit degrees by using the formula : °C=(5/9)· (°F-32). What is x, if x degrees Celsius is equal to x degrees Fahrenheit?

　　(a) 40

　　(b) -40

　　(d) 20

　　(e) -30

　　Answer: x = (5/9)· (x - 32).

　　9·x = 5·(x - 32).

　　In conclusion, x = -40C = -40F

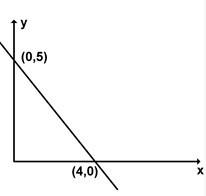
　　Question #6: In the (x,y) plane, what is the equation of the line that passes through the points (0,5) and (4,0)?

　　(a) y = (5/4) · x + 4

　　(b) y = (4/5) · x - 4

　　(d) y = -(5/4) · x + 5

　　(e) y = (5/4) · x + 5

　　Answer: The equation of a line is y = m · x + n

　　First point, x = 0, y = 5, results in 5 = n

　　Second point: x = 4, y = 0, means 0 = m · 4 + n, or m = -n/4 or m= -5/4.

　　In conclusion, y = -(5/4) · x + 5 is the correct answer.

　　Question #7: A square with the side equal to square root of 2 is inscribed in a circle. What is the area outside the square that is inside the circle?

　　(a) ¶ + 1

　　(b) ¶ - 1

　　(d) ¶

　　(e) ¶ + 2

　　Answer: The diagonal of the square is √2 · √2 = (√ 2)2 = 2. This is also the diameter of the circle.

　　The area outside the square and inside the circle is:

　　Areacircle - Areasquare = ¶ · 22/4 - 2 = ¶ - 2

　　Question #8: What is the value of (x + 2y) 2 if x 2 + 4 · y 2 = 2 and x · y = 3

　　(a) 13

　　(b) 14

　　(d) 18

　　(e) 22

　　Answer: (x + 2y) 2 = x 2 + 4 · y 2 + 4 · x · y = 2 + 12 = 14

　　Question #9: What is the value of the median of an equilateral triangle with all sides equal to 5?

　　(a) (5/2) · √3

　　(b) 5 · √3

　　(d) 5/2

　　(e) 5

　　Answer: The median divides the equilateral triangle in two right triangles. Conform to the Pythagorean theorem, wherein the sum of the squares of the two legs is equal to the square of the hypotenuse,

　　m2 + (5/2)2= 52

　　m2 = 52 - (5/2)2 = 52 - 52/4 = (3/4) · 52

　　m = (5/2) · √3.

　　Question #10: A parameter is measured during a scientific experiment and the results are -12, 4, -8, 10, 2, 2, 0, -4 and 2. The median and the average of these numbers are:

　　(a) median = 0, average = -4/9

　　(b) median = 0, average = 4/9

　　(d) median = 2, average = 4/9

　　(e) median = 2, average = 2/9

　　Answer: You must arrange the numbers in order: -12, -8, -4, 0, 2, 2, 2, 4, and 10.

　　The median will be number in the middle of the row, that is 2.

　　The average will be (-12-8-4+0+2+2+2+4+10)/9 = -4/9.

　　以上就是SAT数学Problem Solving练习题(1)的详细内容，考生可针对文中介绍的方法进行有针对性的备考。最后，新东方网SAT频道预祝大家在SAT考试中取得好成绩!

SAT水平能力测试【0元免费测试】